Molecular diffusion
Main features of diffusion:
- is caused by the thermal movement of molecules
- is quantified by a diffusion coefficient, that
=> increases with temperature
=> decreases with increasing molecular mass (proportional to the square root of the molecular mass)
=> depends on the resistance of the medium (water, air ...) - levels out concentration gradients => no net transport if there is no concentration gradient
Have a look at these animations:
Molecules in motion
(Java applet developed by University of California, Regents)
http://chemconnections.org/Java/molecules/index.html
Diffusion
(Java applet developed by Paul O. Lewis, University of Connecticut)
Source: http://hydrodictyon.eeb.uconn.edu/people/plewis/applets/Diffusion/diffusion.html
The diffusive flux F through a cross section is proportional to the cross sectional area, A, the diffusion coefficient, D, and the concentration gradient (Fick's first Law):
F (mol/time) = -A D Δc / Δx (Equation 1)
In a stationary case (i.e., the concentration gradient Δc / Δx and thus the flux F does not change with time) this equation can easily be solved.
Example: diffusion of oxygen from air into blood through a membrane in the lungs. Blood and air are circulated/exchanged quickly and oxygen consumption in our body is ± constant so that the concentration gradient also is constant (neglecting some smaller fluctuations).
Often, however, the diffusive transport does change the concentration gradient (i.e., makes it smaller) and thus affects the flux itself. See for example the second animation referenced above. This non-stationary case is described by the following differential equation (Fick's second Law):
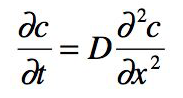 (Equation 2)
(Equation 2)
Note: The physics behind molecular diffusion are always the same, no matter whether we look at a stationary or a non-stationary case, but the mathematics to describe it differ. The second law has analytical solutions only for special boundary conditions. In other cases a numerical solution is needed.
Example for molecular diffusion in a non-stationary case:
A polyethylene film (1 mm thick) is coated on a solid, impenetrable support. This device is submersed into a water sample in order to extract an organic chemical from this sample. The initial concentration in the PE film is zero. The concentration in the water sample is such that the equilibrium concentration in the polymer is one (relative units). Of course with any other numbers the result is just proportional. The capacity of the PE sheet is so small that even the maximal uptake of the chemical into the sheet will not alter the water concentration substantially. In addition, the water is well mixed so that the water concentration at the outside of the PE sheet will always remain constant at 1. For a diffusion coefficient of D= 10-8 cm2/sec the following graph shows the concentration-curves in the PE film at various times after the insertion of the device. Note, that doubling the time does not double the amount of compound that has been transported into the penetrable film (the calculations have been performed with Diffusion.xls).
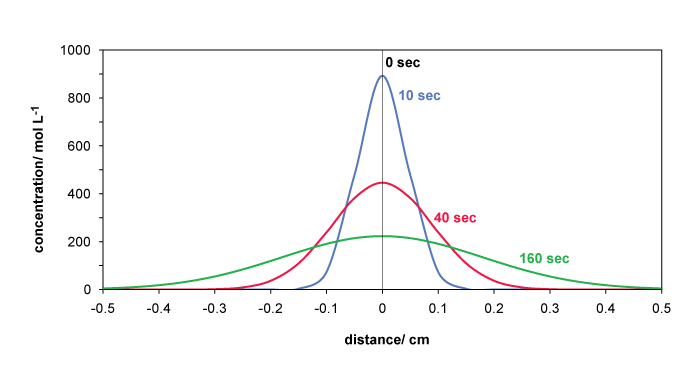
Example for molecular diffusion in a non-stationary case with different boundary and initial conditions:
Imagine a capillary or a pipe with stagnant water in it and a chemical is injected in a perpendicular plane within this pipe. The graphic below shows the concentration-time curves along the pipe as a function of distance from the point of injection for a diffusion coefficient of D = 10-4 cm2/sec which is a typical value in water. The concentration obviously depends on the injected amount but this has no impact on the relative transport curves: if the elapsed time increases by a factor 4, the maximum concentration decreases by a factor 2 and the peak width doubles. So again, this transport behavior is not linear with time.
For an animation of this process (in combination with advection and sorption) see http://research.ce.udel.edu/~imhoff/cieg337/java/ex1.html ![]() and walk.avi.
and walk.avi.
The previous examples show that diffusion in the instationary case is a highly non-linear process: if you double the diffusion time then the travel distance only increases by a factor √2 = 1.4
The following simple equation allows to estimate the characteristic diffusion distance, x, in a non-stationary case without solving any differential equation:
x2 = 2 D t (Equation 3)
This simple equation can be applied to the diffusion process depicted in the figure above as follows: The width of the concentration curve at 0.61 cmax equals 2x =2√2Dt. This band contains 2/3 of all molecules that started at x=0 and t=0. 1/3 of all molecules has travelled further than x at the time t. The decrease of cmax is also proportional to √t.

Equation 3 also allows to estimate characteristic values for the situation in Figure 1. When entering the thickness of the film for x in equation 3 then a time t can be calculated. This time t is close to the time that is needed for equilibration of the film with the outside through the diffusion process. Within this time t roughly 3/4 of the final number of molecules has diffused into the film.
The equation x2 = 2 D t provides a good overview of typical diffusion distances:
| medium | D cm2/sec | time needed to diffuse a given distance x | |||
| 1 µm | 1 mm | 1 cm | 1 m | ||
| air | 10-2 | 0.5 sec | 50 sec | 140 h | |
| water | 10-5 | 8 min | 14 h | 16 y | |
| NAPL | 10-6 | 0.005 sec | 80 min | 140 h | |
| rubbery polymer | 10-9 | 5 sec | 58 d | 16 y | |
Polydimethylsiloxane (PDMS) is a polymer with an exceptionally high permeability. Typical diffusion coefficients for organic molecules are in the order of 5 10-7 cm2/sec. PDMS is often used in analytical chemistry for Solid Phase Micro Extraction (SPME). Equilibration times for typical fiber thicknesses are:
| Time needed to diffuse into a SPME fiber with poly-dimethylsiloxane coating (PDMS) | ||
| 7 µm | 30 µm | 100 µm |
| 1 sec | 30 sec | 3 min |
It follows from the results in the above tables that molecular diffusion is only important for small scale transport processes in stagnant media, e.g.:
- transport on cellular scale in biota
- transport in small pores (soils, sediments)
- transport into polymers
- phase transfer (blood-air, blood-organ, air-water, air-aerosol, water-humic matter ...)
Equation x2 = 2 D t is very helpful for a quick assessment of the effectivity of a diffusion process. However, in some cases more precise information may be required. Here we provide some links that may proof helpful in these cases:
diff-conv const.input.xls
![]()
diff-convect dirac impuls.xls
![]()
Diffusion.xls
![]()
Filter_constant_input_Revised.xls
![]()
Non-reactive and reactive diffusive transport (spherical diffusion):
(Java applet developed by A. J. Valocchi, C. J. Werth, J. J. Decker, G. Hammond, P. Zhou and M. Hafiz)
https://netfiles.uiuc.edu/valocchi/gw_applets/spherical/sphericalGUI.html
![]()
Download this page as a pdf

