Advective transport

... is the transport with another medium, i.e. air or water or with particles that move in air and water themselves.

Main features:

• molecules move at the speed of the medium
• advective transport is not affected by and does not affect any concentration gradients, i.e. a plug of contaminated water will move down a river without any mixing (of course this is not realistic, but for the mathematical treatment it is necessary to separate advection from mixing processes)

Typical velocities:

• rivers: 2-10 km/h e.g. Rhine: ca. one week from Basel to the coast
• groundwater: 3 m/h in gravel to 3 mm/month in clay
• air: intercontinental transport: days to a week
          northern-southern hemisphere exchange: 1-2 y
• sedimentation velocities strongly depend on size and density of the particles

Advective transport always occurs together with:

• molecular diffusion
• dispersion (in case of laminar flow)
• turbulent mixing (in case of turbulent flow)

Dispersion in porous media is an effect of:

• water moving faster in large pores than in small pores
• water moving faster in the middle of a pore than along the wall (due to friction).

Turbulent flow with turbulent mixing typically occurs in air and many natural rivers. It lowers concentration gradients to an extent that some compartments can be treated as well mixed:

• there is a mixing boundary layer in the air close to the terrestrial surface that has a height of ca. 1000 m during day time and 300 m during night time.
• mixing within the troposphere (up to 10 km height) can take days to weeks
• rivers with turbulent flow may be treated as well mixed in the two spatial directions perpendicular to the flow direction.

Mathematically, turbulent mixing and dispersion can be treated as diffusion by just using a dispersion or turbulent diffusion coefficient. (In contrast to molecular diffusion, these coefficients do, of course, not depend on the molecular mass of the transported molecules or temperature.)
E.g. turbulent diffusion coefficients in the ocean:
vertical: 1 cm²/sec
horizontal: 10⁶ - 10⁸ cm²/sec

Due to turbulent mixing a plug of contaminated water will not flow down the river as shown in the animation above but rather like shown here:

Transport in soils can be affected by both processes, dispersion and diffusion. In this case both coefficients can just be added up to be used as a single diffusion/dispersion coefficient in any kind of transport equation. In case of turbulent flow, molecular diffusion can be neglected and only the turbulent diffusion coefficient needs to be known.

Any transport (advective and diffusive) in a mobile phase becomes slowed down if partitioning/sorption into an adjacent stationary phase occurs => retention.

Examples: chromatography, filtration, transport in soil.
(see also animation in the analytical section ).
The equation that covers all transport processes is the advection-diffusion/dispersion equation:

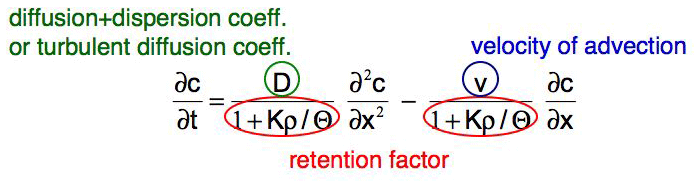
This equation is an extension of Fick's second law (for revision see equation 2 in subchapter "Molecular diffusion" ). Similar to the diffusion process there are some boundary and starting conditions for which this equation has an analytical solution.
See excel sheet diff-convec.xls and http://research.ce.udel.edu/~imhoff/cieg337/java/ex1.html.

In all other cases a numerical solution is needed.

Special case: Preferential flow

Our ability to predict advective transport depends on our understanding of the flow regime of the mobile phase. In soils with macropores preferential flow can occur, leading to an unexpected, fast transport of chemicals deep into the soil. In this case, sorption may be minimal because surface contact is minimal.

Download this page as a pdf