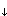Problem 1

Imagine the following situation: There is a lake with well mixed water. In the sediment at 1 m depth below the sediment-water-interface, methane production by bacteria is going on. Thus methane is diffusing into the lake where it is quickly diluted due to turbulent mixing, and then gassing out at the lake surface (here we ignore all processes that may consume methane). What is the concentration profile of methane between the layer where it is produced and the sediment-water-interface (neglect what is happening further down in the sediment)?

Hint: You can solve this mathematically but you can also solve it by some simple plausibility considerations.

Answer: As soon as methane is produced, a concentration gradient towards the sediment-water-interface develops and diffusion will start. Imagine that the production rate is higher than the diffusion rate. In this case, the methane concentration in the layer where it is produced will rise. What does that mean for the diffusive transport? => It will also rise because the concentration gradient rises (see Fick's first law). In fact, the rate of diffusion will rise as long as the concentration in the methane production layer increases until - eventually - the rate of production equals the rate of diffusion. Hence, sooner or later, the system will reach a steady state situation unless it is disturbed from the outside (e.g. by temperature fluctuations). If we have a steady state flux, what does that mean for the concentration gradient? => A constant flux through the various layers of the sediment implies a constant gradient according to Fick's law if we assume that D is constant. Hence, the concentration profile would follow a straight line between the steady-state concentration in the layer of production and the steady-state concentration in the lake water at the sediment-water-interface.

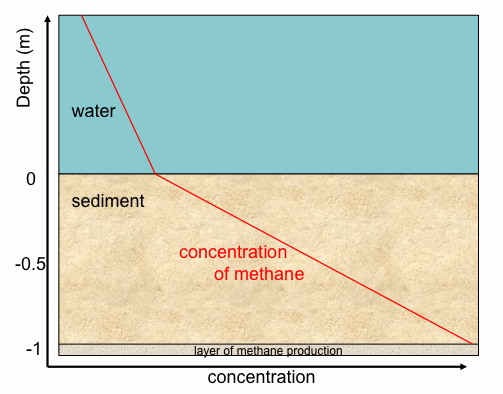
What is this knowledge good for? If you measure the concentration gradient in a lake sediment and you find it to be constant you can:

a) conclude that sediment was in a steady state situation (i.e. production rate = diffusion rate) and you can

b) calculate the production rate because it is equal to the diffusive flux rate which can be estimated from the measured gradient, the known diffusion coefficient and the estimated or known porosity.

Add-on question 1: How would the system respond if - due to some temporary external disturbance - the concentration gradient was not linear but had the following form ?:

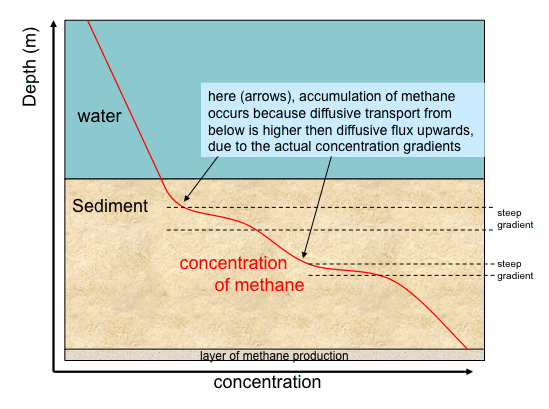
Along the steeper gradient (i.e. large change in concentration on a small vertical distance) diffusion would be faster than along the shallow gradient so that methane would accumulate wherever a steep gradient becomes shallow. Thus diffusion would level out differences in the concentration gradient with the effect that a constant gradient would develop again.

Add-on question 2: How would the concentration gradient look like if there was methane consumption going on at 50 cm depth below the sediment-water-interface?

Add-on question 3: How would the concentration gradient look like if the porosity was not homogenous throughout the depth of the sediment but had the following structure?

-1 m to -0.6 m : porosity 0.85

-0.6 m to -0.4 m : porosity 0.45

-0.4 m to -0.0 m : porosity 0.85 As you can see, one can learn a lot about ongoing environmental processes from just measuring the methane concentration gradient plus the porosity in a lake sediment if one understands the concept of diffusion.

Download this page as a pdf