Fragment models

Figure 1 shows air/water partition constants at 25°C for various homologue compound classes.
Obviously, there are striking regularities to be seen, all compound classes exhibit more or less the same slope. In other words, a CH₂-fragment added to a molecule always adds a constant increment to the respective log K_{i air/water}

Roll over the image to see the CH₂-increments.


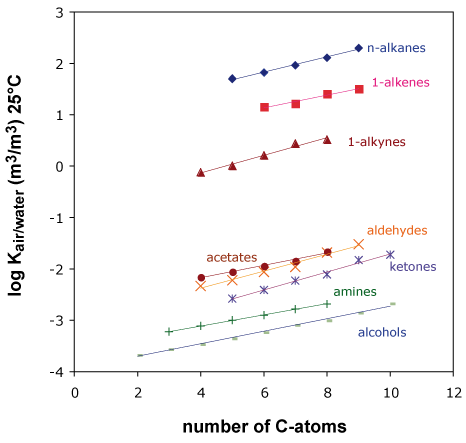
Figure 1

For example, the value for n-hexane differs from n-pentane by 0.12 log units. The same difference can also be seen between n-heptane and n-hexane, between n-hexanol and n-pentanol and so on.
Similarly, the substitution of one hydrogen by a hydroxyl-group adds a constant increment to the air/water partition constant, no matter whether this substitution occurs at pentane or hexane or heptane.

Roll over the image to see the OH-increments in Figure 2.

The same regular behavior is found for other functional groups like the keto, ether or aldehyde groups. Please see Problem 1.

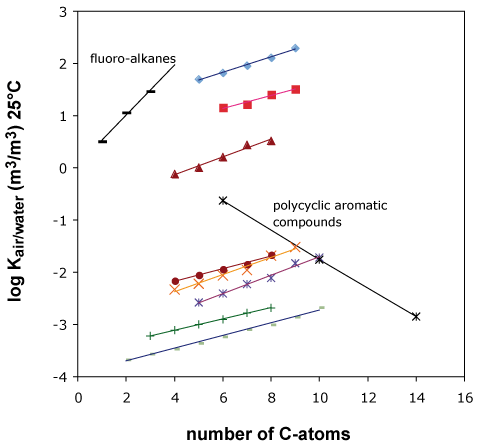
Figure 3

The increment for an aromatic ring is negative, similar to the increments of a keto- or a hydroxy-group, because these groups increase the tendency of the molecule to stay in water.

Using a large data set of air/water partition data, one can derive a collection of logarithmic air/water partition increments for various molecular fragments. For new molecules that are built of known fragments one can then calculate the air/water partition constant by adding up all required increment-values. Please see Questions for recapitulation.

Models that predict partition constants based on this principle are called ‘fragment models’. The experimental data used for deriving the incremental values are called the ‘calibration data set’. Such fragment models have the advantage that they only require knowledge of the molecular structure of the compound and principally they can be applied for all types of partitioning. However, reality is more complex than the data in the figures above may have suggested. Fragments do not always behave additively as you will see when you try to answer Question 3 of the selftest.

Two functional groups that occur close to each other in a molecule can affect each other such that their single contribution to the partitioning of the whole molecule is not additive any more.
Current fragment methods try to account for such effects either by correction factors or by treating the whole molecular increment that contains the functional groups as a single increment, e.g. the dione-increment in the software KOCWIN^TM.
This is the link to the website where you can download the software (runs on windows): http://www.epa.gov/oppt/exposure/pubs/episuitedl.htm.

Figure 4 illustrates non-additive effects for various bifunctional aliphatic molecules in which CH₂ increments are added between the functional groups. The effect is quite erratic and completely different from adding CH₂ increments to a simple alkanol, which is shown for comparison.

Many chemicals of environmental concern are quite complex (see the structures of the pesticides Parathion and Monuron as an example).

Good fragment methods that can deal with this complexity therefore require a multitude of correction factors and/or increments that can only be derived from a large and diverse calibration data set. If certain molecular structures are not represented in the calibration data set, then compounds containing such structures should not be calculated with this model, i.e. these compounds do not fall into the applicability domain of this specific model.
Such complex fragment models typically come as a complete software where you enter the structure of a compound and the software does the fragmentation and calculation. Unfortunately, in most cases the user has no access to the calibration data set and therefore no means to judge its applicability domain.

Download this page as a pdf