Poly-parameter Linear Free Energy Relationships (pp-LFERs)

These pp-LFERs work for polar and non-polar compounds alike because they contain separate descriptors for the various intermolecular interactions that may occur between the sorbate and the phases. The figure below shows the principal structure of these models:

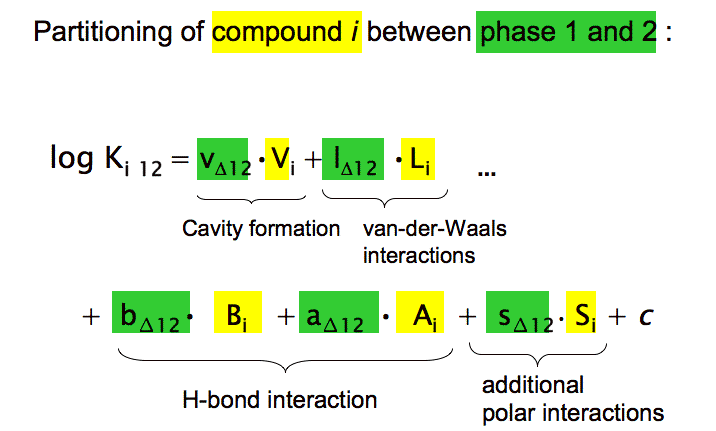
Each interaction energy is reflected by a separate term that consists of the product of two variables, one describing the compound property (e.g. molecular volume, V_i, in the cavity term) and the other describing the complementary system properties (e.g. the cohesive energy difference between phases 1 and 2, v_Δ12). It should be obvious that these pp-LFERs are nothing else than the quantitative analogue to the qualitative model that was developed in Chapter 4. However, besides the H-bond interactions, the pp-LFERs contain an additional type of electrostatic interactions (described by s₁₂ S_i) that we had omitted for simplicity reasons in Chapter 4 but that is required for good quantitative predictions.

The other descriptors denote:
   B_i - H-bond accepting property of the compound
   A_i - H-bond donating property of the compound
   a_Δ12 - difference in the H-bond accepting properties of phases 1 and 2
   b_Δ12 - difference in the H-bond donating properties of phases 1 and 2
   L_i - the hexadecane/air partition constant of the chemical at 25 °C
   l_Δ12 - the difference in the combined cavity /vdW energy of the phases

Both energies, van der Waals and cavity strongly depend on the size of the solute. Hence, in most cases where a pp-LFER equation is calibrated for a specific system it is statistically not feasable to clearly distinguish the cavity energy contributions from the vdW contributions. Hence, in practice both terms v_Δ12 V_i and l_Δ12 L_i contribute to both interaction energies to some degree.

pp-LFERs can be used for any partition system and any compound whose descriptor values are tabulated. For a selection of compound descriptors (capital letters) see Table 9, for system descriptors see Table 10, 11 and Box 11 in the textbook.
System descriptors are typically derived by a multiple linear regression of the above equation to a calibration data set with known compound descriptors and known log K_i12 values. In this multiple linear regression the system descriptors are the unknowns. Note that in practice it is not a trivial task to assemble a calibration data set that is as diverse as required (see problem 6).

In the literature one finds slightly different forms of pp-LFER equations:
- some terms may be missing because they are not relevant for a specific partition process
- van der Waals and cavity interaction energy may be described by various parameter combinations like: L and V (used here), L and E (E is related to the refractive index of a chemical) or V and E.

Note that the system descriptors are temperature-dependent.

Examples for the application of pp-LFER equations can be found in chapters VI and XI.1 in the textbook.

Download this page as a pdf