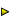Equilibrium partitioning and the free energy of partitioning

All what we have said so far about the equilibrium partitioning of a chemical between various phases is captured by the following fundamental equation that relates the energy of interaction of i in two phases 1 and 2 to its partition constant, K_{i 12} at a given temperature:

₁₂ G_i = -R T ln K_{i 12}        (2)

where ₁₂ G_i (J/mol) is the difference in the interaction energies per mol of i in the two phases 1 and 2. R is the universal gas constant (J/(mol K)) and T is the absolute temperature (K). This free energy is identical to the work that needs to be invested into the system to transfer one mol of i from phase 2 to phase 1.

We can evaluate equation (2) in order to see whether it is consistent with our previous understanding of partition equilibria: If the interaction energy is equal in both phases then the partition constant will be unity, i.e., the equilibrium concentrations of i in both phases 1 and 2 will be the same. If the interaction energy of molecule i in phase 1 is larger than the energy of i in phase 2 then energy is gained from the transfer of molecules i from phase 2 to phase 1 and ₁₂ G_i is negative. In this case, K_{i 12} will be larger than unity which means that c*_{i 1} > c*_{i 2}. This shows that equation 1 is indeed in agreement with what we expect from the qualitative discussion on equilibrium concentrations.

Download this page as a pdf