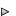The cavity approach

Step 1: The first step that is involved in the partitioning of a compound i into a phase is the creation of a cavity in this phase. This cavity is required to volumetrically accommodate the molecule i . This step requires energy to separate the phase molecules from each other. The free energy required for the cavity formation depends on the interaction energy between the molecules that make up the phase and it depends on the size of the required cavity — i.e. the size of molecule i . The higher this cavity-energy the smaller is the equilibrium concentration of i in the respective phase unless it is compensated by other interactions (see step 2).

Step 2: In the second step, molecule i is placed inside the cavity. Free energy is released in this step by the newly formed interactions between molecule i and the phase molecules that surround i . This interaction energy favors the partitioning into the respective phase.

These 2 steps have to be considered in any bulk phase (with the exception of air where no interactions take place) that is involved in the partition process. In the phase that is left by a molecule the energies obviously must have an opposite sign: here energy is required to break up the interactions between the solute and the surrounding phase and energy is gained when the remaining cavity closes after the solute has left the phase.

It is obvious that any reasonable understanding of equilibrium partitioning does require at least some basic information about the intermolecular interactions that occur in steps 1 and 2.

Download this page as a pdf